Origin and Correction of the Spherical Aberration of Electron Lenses

The spherical aberration of round electron lenses is unavoidable because the outer zones of these lenses refract the electrons more strongly towards the optic axis than the inner zones, as depicted in Fig. 1. As a result, the image of each point of the object plane is a disc whose radius determines the resolution. Unfortunately, the rays passing through the outer zones of the lenses cannot be removed by an aperture because large aperture angles θ are necessary in order to prevent that the diffraction limits the resolution due to the wave property of the electrons.

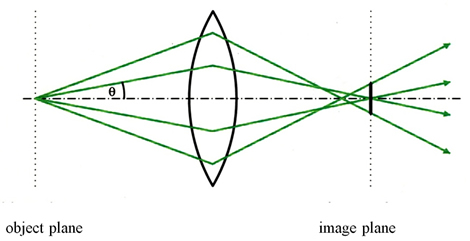
Figure 1: Schematic course of the trajectories of electrons which start with different slopes from the center of the object plane and are focused by a round electron lens. Click image to enlarge.

Principle of the corrector compensating for the spherical aberration
The corrected system depicted in Fig. 2 is composed of the objective lens, the telescopic transfer doublet, and the so-called hexapole corrector. It consists of two sextupoles (hexapoles) S1 and S2 and another telescopic round lens doublet formed by two identical round lenses separated from each other by twice their focal length f. Die doublet reverses the course of the paraxial trajectories images the sextupole S1 located at the front-focal plane of the first lens with magnification -1 onto the second sextupole S2 placed at the back focal plane of the second lens.

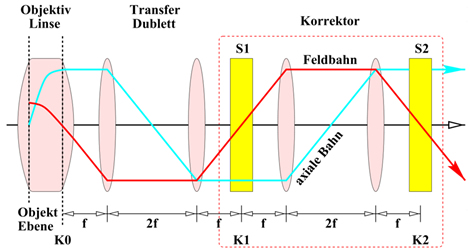
Figure 2: Course of the paraxial field ray (Feldbahn) and of the axial ray within the corrected system consisting of the objective lens, the telescopic round-lens doublet, and the corrector. This system is the main component of most commercial corrected electron microscopes. Click image to enlarge.

In this case the non-rotationally symmetric deviations produced by the two sextupoles nullify each other whereas their rotationally symmetric aberrations add up. The sign of the spherical aberration is opposite to that of the round lenses and proportional to the square of the sextupole strength which is chosen in such that the spherical aberration of the entire system vanishes. Since the corrector does not affect the paraxial rays and deflects the non-paraxial rays away from the optic axis it acts like glasses compensating for the poor imaging property of the round lenses as illustrated in Fig. 3.

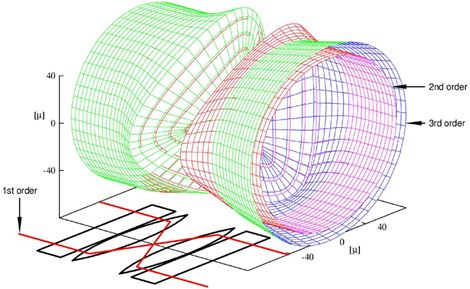
Figure 3: Action of the sextupole (hexapole) corrector on electrons which propagate initially parallel to the optic axis on the mantle of a cylinder. The paraxial rays (1st-order approximation) travel again parallel to the optic axis in the region behind the corrector. The threefold 2nd -order ray deviations vanish in this region whereas the 3rd-order deviations are located on the mantel of a rotationally symmetric cone. These deviations are forming a negative spherical aberration at the image plane whose strength is proportional to the cone angle. This angle can be adjusted by means of the sextupole strengths such that the spherical aberration of the entire system is nullified. Click image to enlarge.